اين آزمون براي ارزيابي ميزان همقوارگي يا يكسان بودن و يكسان نبودن (Goodness of fit) ميانگين نمونه اي x̅ و ميانگين جامعه یعنی µ به كار مي رود.
اين آزمون مواقعي به كار مي رود كه مي خواهيم بدانيم آيا ميانگين برآورد شده نمونه اي x̅ با ميانگين جامعه یعنی µ جور مي آيد يا نه. اگر تفاوت این دو كم باشد، اين تفاوت معلول تغيير پذيري نمونه اي شناخته مي شود، ولي اگر زياد باشد نتيجه گرفته مي شود كه برآورد نمونه اي با پارامتر جامعه يكسان (همقواره) نيست.
آماره این آزمون به قرار زیر است:
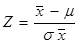
كه در آن µ = ميانگين جامعه و x̅ = ميانگين برآورد شده نمونه اي
و σ x̅ = خطاي استاندارد نمونه اي است که از فرمول زیر بدست می آید:
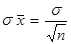
كه در آن σ = انحراف معيار توزيع متغير در جامعه و n = تعداد نمونه است.
اين آزمون پارامتري يا پارامتريک است يعني استفاده از آن مشروط به آن است كه دو پارامتر جامعه كه µ و σ باشند، معلوم باشند.
همچنين این آزمون براي متغيرهاي پيوسته (مقياس فاصله اي) كاربرد دارد و بایستی تعداد نمونه n بزرگتر و يا مساوي 30 باشد و نيز توزيع متغير در جامعه نرمال باشد.
براي انجام تحلیل آماری پایان نامه با استفاده از آزمون z (آزمون زد) و سایر آزمون های آماری از طریق مبادی ارتباطی درج شده در پایین صفحات سایت با ما تماس بگيريد یا فرم سفارش تحلیل آماری را تکمیل نمایید.
چنانچه مايليد در خصوص آزمون z بيشتر بدانيد مقالات زير از سايت اصلي اين مرکز آماري را مطالعه نماييد:
آزمون z : مقایسه ی یک نسبت با عدد ثابت ( با فرمول و مثال)
آزمون z: تساوي دو نسبت (با فرمول و مثال)
آزمون z : مقايسه ضريب همبستگي با عدد ثابت ( با فرمول و مثال)


سلام. لطفا سوالات و نظرات خود در خصوص اين مطلب را در همين بخش ديدگاه مطرح نماييد. از طريق ايميل از پاسخ ما مطلع خواهيد شد.
براي جستجو در ميان کامنت ها از Ctrl + f استفاده نماييد.
سلام چه زمانی از z test و چ زمانی از t test باید استفاده کنیم در واقعیت و چ زمانی ازمون t test به سمت ازمون ztest میرود؟؟؟
سلام. در نرم افزار SPSS عملا آزمون z نداریم و از همان ازمون t استفاده می گردد. زیرا اگر داده ها نرمال باشند، با دقت بالایی نتایج همانند آزمون z بدست می آید. و اگر هم نرمال نباشند که خود آزمون t بایستی اجرا شود.